How is Euclid Implemented?
The current version of Euclid is only a
prototype to a feasibility study. It does solve all of the
examples presented here but
it is inefficient and slow. The bulk of the code is written
in Quintus Prolog (Release 3.2) and C: about 15,000 lines
of prolog code and 3,000 lines of C code. For solving mathematical
equalities/disequalities, Euclid relies on Mathematica(TM)
and CLP(R) which are connected to the main program engine
using a UNIX pipe interface. The system runs on a Sparc
processor under SunOS 4.1.3_U1 from an executable of 1.4MB
in size. The language is supplied as an interepreter with
mininal internal editing facilities and the standard prolog
like prompt interface.
The prolog code for the interepreter provides
a good presentation of the operational semantics. Alas,
the more readable the code, the less efficient it is. Many
other limitations and problems creep up in the current implementation
many of them inherited from the underlying programming systems
(e.g. mathematica bugs are very frequent and there is no
solution to them). Because the code is in pre-alpha version
(and also since any system wishing to test the language
should have Mathematica and CLP(R) available) the
code is not currently available but a test version could
be made available in the near future to Academic Institutions
and research centers. You may use this form
to request the source code.
How about future Implementations?
A proper implementation of Euclid should
not rely on any external solvers. An extension to the WAM
or CLAM machines could be created and the code re-written
in C to allow compilation as well as interpretation of source
code. Many extensions to the language are visible and easily
implementable. Such an implementation could supply a good
platform for programming with mathematics using also higher
level I/O primitives for graphics and file access.
Naturally any proper implementation of
Euclid should rely on a sophisticated user interface, both
for editing programs as well as for presenting answers to
queries. Such an interface should be based on a GUI environment
with tools such as Equation Editor and TeX/postscript output.
This way the code fragment:
lorentz([X,T],[X1,T1],U,C):-
reals([X,T,X1,T1,U,C]),
G=sqrt(1-(U/C)^2),
X1=G*(X-U*T),
T1=G*(T-(U/C^2)*X).
will be entered/viewed as:
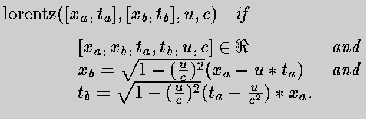
I am currently trying to put together a
project that will fund the development of the language as
a research tool for problem solving or even as a viable
commercial product.