A number of Examples currently running
on Euclid
Here are a number of examples in Euclid.
For each example the source code is given together with
a sample session. Remember than in euclid we use constraints
to describe situations in our model and logic to
define the applicability of constraints.
Contents
Scientific Knowledge Representation
Interacting Component Systems
Suppose that we have to control a train,
traveling on a single (straight line) track between towns
A and B. We are bound by the following constraints: The
train can travel with a maximum speed Umax and for maximum
comfort of the passenger it can only accelerate (and decelerate)
with Acc. The train should automatically accelerate to the
maximum speed (if the distance permits it) and then at the
proper time start decelerating in order to reach station
B at zero speed.
For the solution of this problem we use
a function to describe the velocity of the train as it changes
in time. It is clear that two situations will arise: i.
either the train will have time to reach Umax, in which
case there will be 3 distinct intervals (acceleration, cruising,
deceleration) or ii. it will reach a speed lower than Umax
and then start to decelerate (i.e. 2 intervals acceleration,
deceleration). In the program we let the system decide how
the function will look like using the 'combine' operator
#/2.
The method for soving this problem can
be viewed in the commented Euclid
Source Code as well as the Sample
session in Euclid producing the desired output.
top of page
The next example is from the realm of physics
and specifically about falling bodies. This example is particularly
interesting because it proves the inability of common sense
reasoning to deal with physical situations. Suppose from
the top floor of a very tall building we let fall a bowling
ball and a feather at the same time (and without any initial
speed). Which object is going to reach the ground first?
Most people would answer (correctly) that the bowling ball
will be the first one to crash on the ground. Unfortunately,
most people would give the right answer for the wrong reason
(most people believe that heavier objects fall at a greater
speed). To demonstrate the falsehood of this claim, Eötvos
performed the same experiment inside a crystal tube after
he has extracted all the air with a pump. To the spectators
astonishment, both the heavy ball and the feather reached
the ground at the same time.
The problem in this case is to find the
difference in time between the two objects (short) flights.
The Source
Code is based on object kinematics and dynamics and
defines generic relations to describe this. The output
of the sample session shows that both
times are equal.
top of page
This problem is taken from elementary physics
oscillations. Suppose that we have managed to dig a tunnel
passing through the center of the earth from side to side.
Then, (how novel!) we decide to drop a ball in the shaft
and watch its motions. What will it do? Will it come out
the other side? Will it end up at the center?
The interesting part of this problem is
the ability of the language to cope with knowledge from
the field of mathematics. The equations that govern the
phenomenon are easily coded into Euclid (see the Source
Code and the problem is solved in its most general case
(see the output).
top of page
Another problem which is easily solved
using piece-wise modeling methods is that of the leaking
tanks. A number of tanks (depending on the exact configuration)
are adjacent to each other and their walls can develop holes
from where fluid might start to flow into another tank.
It is also possible (in the more general case) that a wall
might completely collapse when the liquid becomes to heavy.
In our case, two tanks are defined: the
inner and outer tanks. Each one is considered as a system
with specific input and output. The problem is solved by
connecting the output of one tank with the input of another.
The Source
Code explains
the problem in more details and the Euclid session
output
shows the two possible solutions as
multi-branch functions of time. Note that at a future version
of Euclid the output could be easily beautified (e.g. as
direct graphics/postscript output).
top of page
Finally we present an example from special
relativity, the famous twin paradox. In this example it
is not the paradox that we are really interested in. It
is rather the explanation given by the special theory of
relativity.
Suppose that two twin brothers (born at
the same time) find themselves in the following situation:
one brother is an astronaut ready to try the new interstellar
spaceship on his trip to Alpha Centauri. The trip should
not last long with the new engines which allow instant acceleration
to .8 of the speed of light (i.e. around 240,000Km/h) and
decelerate at the same speed. In the mean time, the other
brother remains a happy farmer on mother Earth. After the
trip (which took according to the astronaut only 10 years)
his brother on earth is now 16 years older.
This calculation is based on the lorentz
transformation:
lorentz([X,T],[X1,T1],U,C):-
reals([X,T,X1,T1,U,C]),
G=sqrt(1-(U/C)^2),
X1=G*(X-U*T),
T1=G*(T-(U/C^2)*X).
describing the relation between the coordinates
of the 2 systems moving relative to each at speed U. According
to the theory, time dilation can then be calculated by:
time_dilation(T,T1,U,C):-
reals([T,T1,U,C,XA,TA,XA1,TA1,XB,TB,XB1,TB1]),
XA=XB,
T=TA-TB,
T1=TA1-TB1,
lorentz([XA,TA],[X1,TA1],U,C),
lorentz([XB,TB],[XB1,TB1],U,C).
By posing the query
euclid ?- time_dilation(T,10,0.8*C,C).
we get the answer
[C]:reals
T=16.6667
More (y/n) y
*** No ***
top of page
This problem has been chosen as a representative
of a wider class of problems: systems which are made up
of interacting components each of which can be precisely
modeled mathematically. In the case of electrical circuits,
the components (resistors, capacitors, sources etc) are
connected together to form circuits which are governed by
local and global laws (The Kirchoff Laws).
The user is only required to descrive the
circuit; the problem is solved by transforming the circuit
into an internal representation form and applying to it
the governing laws. Each component is described seperetly
by a predicate constraining the drop in voltage between
its ends and the current passing through it. The Source
Code
is able to handle generic circuits of both AC/DC sources
by representing currents and voltages with real formulae
(see the guide to available domains
for more information on real formulae and the constraints
defined in that domain). The program has been tested on
several simple circuits with interesting results
escpecially
in case like the RC-circuit or the Wheatstone brige.
Some of the examples concidered are:
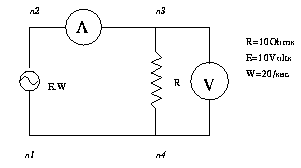 ,
, 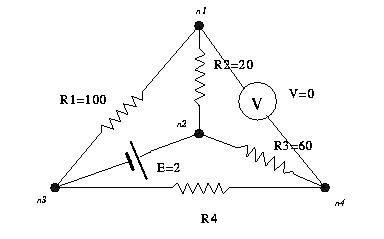 and
and 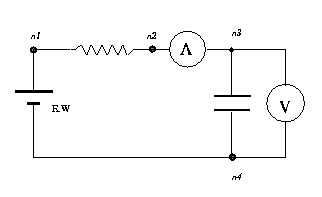 .
.
This program does not include code for
calculating closed non-directed loops on the circuit as
required by Kirchoff's Law of voltages. Implementation of
such an algorithm is outside the scope of this example;
any implementation of the widely available algorithms would
follow the prolog programming paradigm.